
The difference between kW (kilowatts) and kWh (kilowatt-hours) is one of the most misunderstood, and hence, widely discussed topics in the solar industry. However, energy literacy is not just a matter of semantics, but also economics.
The layperson can be forgiven for mixing up these two important metrics, but perhaps we shouldn’t be so lenient with solar salespeople, energy professionals, and journalists when talking all things electrical. Misusing these terms shows either a lack of understanding or care. Even a casual typo could end up being an expensive one.
Rather than deep diving into the technicalities of physics, this article will cover:
- A simple explanation of the terms kW (kilowatt) and kWh (kilowatt-hour).
- Examples of power and energy relating to appliances, household consumption, rooftop solar, home batteries, and electric vehicles.
- The most common mistakes made when talking about these terms.
- Why it helps to know the difference, and how it can save you money.
kW And kWh – A Simple Explanation
SolarQuotes founder Finn Peacock has already written extensively on this subject1. These articles are still relevant and well worth reading. Here’s another take to help get the message through.
kW (kilowatt)
kW (kilowatt) is a measure of power. Power in electrical terms it is the rate at which electrical energy is transferred in an electric circuit.
If an electrical appliance is powerful, its power rating (measured in kW) will be high, and it will consume electricity quickly.
kWh (kilowatt-hour)
A kWh (kilowatt-hour) is a measure of energy. Energy in electrical terms is the ability or capacity to store and transfer that electricity over a period of time.
If you leave the appliance above on for a long time it will use a lot of energy, which can be measured in kWh.
h (hour)
Stating the obvious but still relevant – an h (hour) is a measure of time. You already know what time is.
In this case, we’re talking about the time the above appliance is running. We need to know this because it ties all the power and energy stuff together.
Electrical Energy Equation
Here is a simple mathematical equation that shows the relationship between power (kW), energy (kWh), and time (h). Yes, it sounds boring, but stick with me, and you’ll be forever grateful.
Power (kW) x Time (h) = Energy (kWh)
That’s it. So simple it’s even in the name! kW x h = kWh. That’s all you need to know. I could finish here but I’ll keep rambling on and trying to empower you. I hope you have enough time to listen and don’t run out of energy (reader rolls eyes).
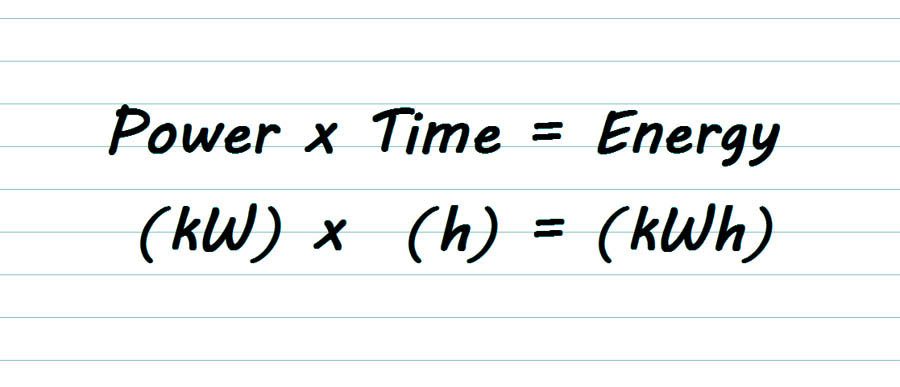
Examples Of Power And Energy
Electrical Appliance Example
In our appliance example above, let’s assume the power rating (on the nameplate) is 2kW, and the appliance runs for 4 hours. Using the electrical energy equation, it’s easy to see that the appliance uses 8kWh of energy.
Power (2kW) x Time (4h) = Energy (8kWh)
Shown on a graph, the Energy consumed is the area under the line.
It looks like this:
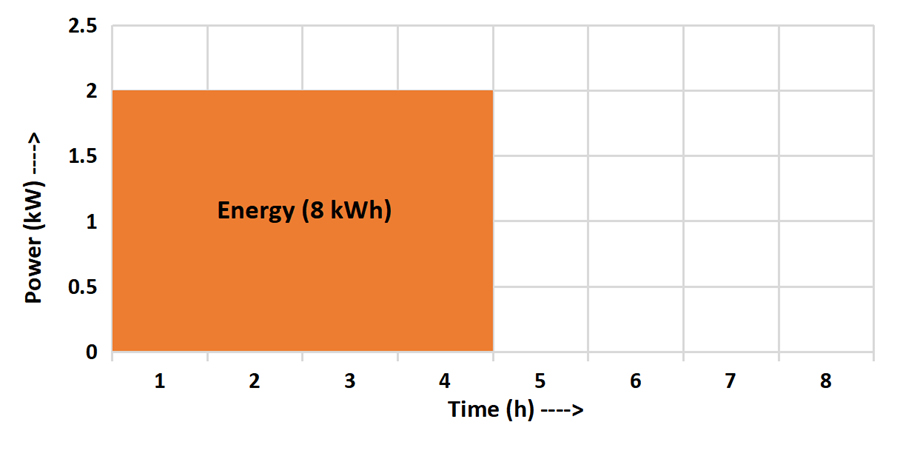
Similarly, an appliance rated at 1kW would use the same amount of energy (8kWh) if it ran for 8 hours.
Power (1kW) x Time (8h) = Energy (8kWh)
Electrical Appliance Example Take 2
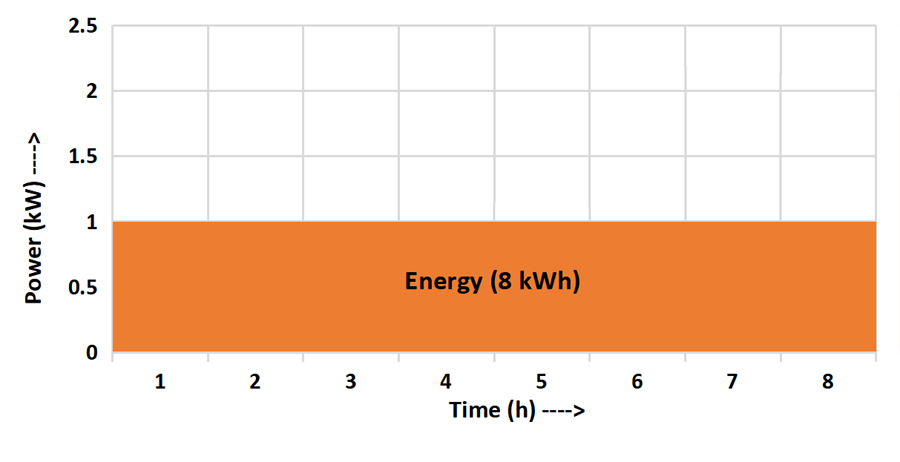
Let’s muddy the waters a little. Although a nameplate may specify 2kW, that usually refers to peak power or the maximum rate it will consume energy. In reality, most electrical appliances use power at varying rates.
A washing machine may use different rates of power on different cycles, such as heating the water, washing, and spinning cycles. A full load will use more power than a half-full load. In this case (and in all cases), the electrical energy equation uses average power over the given time.
If an appliance rated at 2kW peak power runs at 2kW for the first hour, 1kW for the second hour, 2kW for the third hour, and 1kW for the fourth hour, the average power would be 1.5kW (2kW + 1kW + 2kW + 1kW = 6kW divided by 4 hours)
The electrical energy equation would then be Power (1.5kW) x Time (4h) = Energy (6kWh)
Shown on a graph, it would look something like this:
Note that an appliance rarely runs at a particular power rating in neat little chunks of 1-hour blocks, as shown on the graph. This is only to get the point across.
Household Energy Consumption Example
Your household uses many appliances that mostly run at varying rates of power at different times of the day. On top of that, many are constantly being switched on and off. Inputting the data into a mathematics equation would get complicated very quickly. It’s more easily shown on a graph or an app. This graph shows peak times of energy usage in the morning and evening.
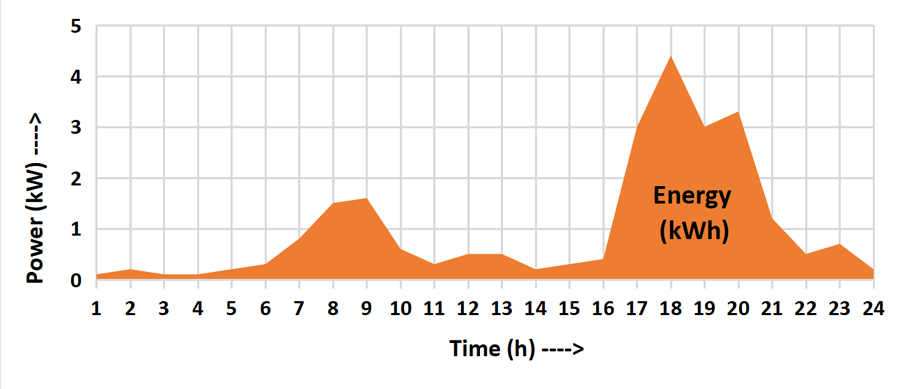
Your energy provider usually charges you for the energy (kWh) you use over the billing period – not the power (kW). Notice I said *usually*. Hold that thought – more on that later.
Rooftop Solar System Example
kW and kWh are used as a unit of measure for electricity generation and consumption. A rooftop solar power system, being a generator, is rated by the peak power of the solar array.
A solar array produces power at varying rates over a given time. This is because the output depends on factors such as location, weather, time of year, shading, efficiency, etc. It’s unlikely to hit the peak power (kW) for very long, if at all.
The following example uses a solar array rated at 5kW. You can see in the graph below that although the peak power is 5kW, the energy produced in 24 hours is NOT 5kW x 24hrs. That would be 120kWh! Instead, as in the previous examples, the calculation is based on average power over 24 hours:
0.2kW (average power) x 24hrs (time) = 20kWh (energy)
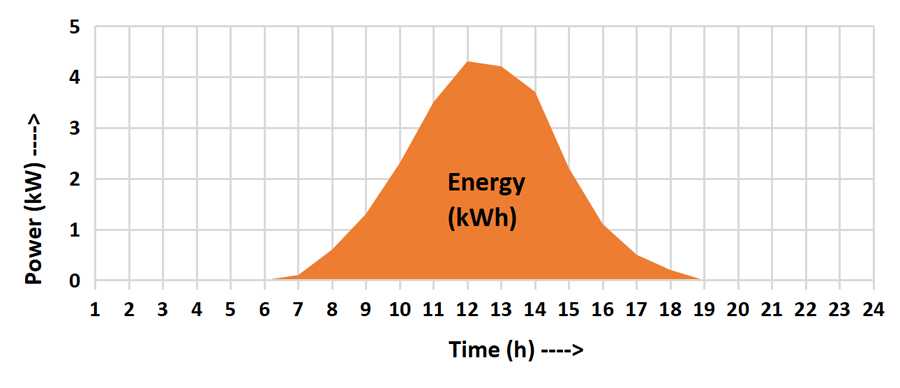
Fortunately, thanks to satellites and some very clever people, there is good data available that will predict the likely solar energy available at any given location on Earth. They’ve worked out that if installed correctly, 1kW of solar power will produce approximately 4kWh of energy per day in most parts of Australia. Here’s another equation that gives the same result as above:
5kW (solar array peak power) x 4 (average energy per kW over 24 hours) = 20kWh (estimated energy)
Home Battery Example
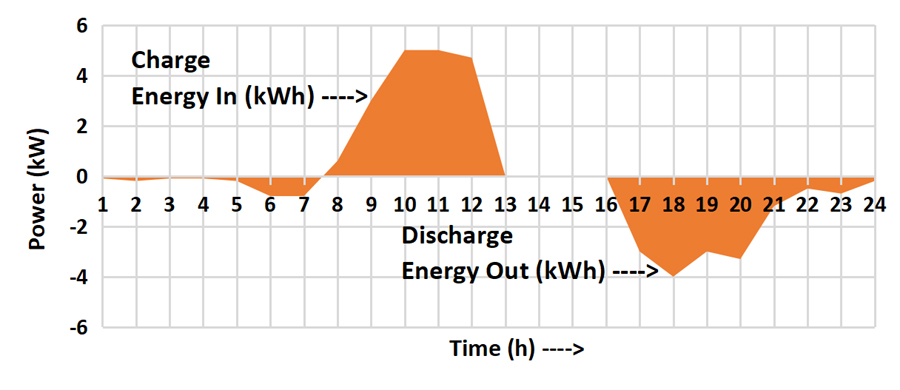
The size of a home battery is shown in kWh (kilowatt-hours). The is the usable energy or capacity of the battery. There is also a power rating if you dig into the datasheet. For example, a 10kWh battery may have a power rating of 5kW peak power. This means if it were discharging at the fastest possible rate (5kW) the 10kWh battery would be empty in 2 hours.
Of course, that rarely happens because batteries charge and discharge at varying rates. The following graph shows energy (kWh) flows both ways as a battery discharges, recharges, and discharges again over 24 hours. The battery S.O.C. (state of charge) can be determined by adding up the energy in and out, and a whole bunch of other stuff that we’ll save for another day.
Electric Vehicle Example
EVs also have a power (kW) and an energy (kWh) specification. Obvious to you by now, the power rating relates to the motor and the energy capacity of the battery. EV buyers pay particular attention to the size of the fuel tank (battery), which is given in kWh. Most petrol car owners couldn’t even tell you the size of their fuel tank.
Common Misuses Of The Terms kW (kilowatt) And kWh (kilowatt-hour)
Believe it or not, I’ve found the following statements and/or questions on blog comments and social media forums. Let me know if I can add any more to the list.
“My solar panels produced 18kW of electricity yesterday.”
Um, no they didn’t. They produced 18kWh of electricity yesterday.
“Hello all, hoping to get some advice on this quote. It’s a small unit, using 5kW per day max.”
The quote they got was for a 5kW rooftop solar system! This is a classic mistake that could cost this person big dollars for no good reason if they meant 5kWh per day. This is almost certainly what they meant because 5kW per day makes no sense, and 5kWh per day consumption, although low, is quite possible for 1 or 2 people in a small unit.
“The nameplate on my dryer has 2.4kW stamped on it. Does this mean I need to be generating 2.4kWh to run the machine?”
The short answer is “no”. The person may or may not have interchanged the terms kW and kWh, so assumptions have to be made. If they are asking what the rate of power (kW) the machine uses, the answer is that it will pull 2.4kW maximum through its cycle but most likely average much less. If the person was asking about the energy (kWh) consumption the answer is still “no” because it depends on how long the dryer runs. Remember this simple equation, kWh = kW x h.
“If a solar panel produces energy of 4kWh per day does it mean that it is producing the 4kW of power every hour? If it is so it will generate 96kWh of energy for the whole day? Or is it producing 4kWh of energy in the whole day which means 0.166 kWh of energy every hour?”
She answered this for herself. The second guess was almost correct. It produces 4kWh of energy in the whole day, which means AN AVERAGE of 0.166 kWh of energy every hour.
“My daily household electricity consumption is 12 kilowatt/hours per day.”
No, it’s not. It is 12 kilowatt-hours (kWh) per day. kilowatt/hours means kilowatts per hour. Kilowatt-hours is the term used to measure energy, being a product of kilowatts and hours. Kilowatt/hours and kilowatt-hours mean vastly different things.
Tomatoes, Tomartos, kilowatts, kilowatt-hours, Who Cares?
Not me. You make your bed, you lay in it. Here are some reasons YOU should care though:
- As pointed out above, if you get kW and kWh mixed up, you might buy a rooftop solar system 4 or 5 times larger than needed. That’s a multi-thousand-dollar mistake.
- Most people buy solar and/or batteries for financial reasons, so minimizing the payback time is a priority. Maximizing self-consumption is the key, and the best way to do that is to understand how you use energy so you can use the right appliances at the right time.
- Earlier in this article, I mentioned how your energy provider *usually* charges you for the energy (kWh) you use over the billing period – not the power (kW). Well, that’s not always the case. Many businesses and some residential customers also get charged for peak power usage. This is known as demand pricing. Avoid being moved to one of these plans if possible. Understanding your power and energy will help immensely.
- The other reason it’s good to differentiate between kW and kWh is for your vanity. It can be quite embarrassing attempting to talk to people about your new solar and battery system, but only mumble meaningless technobabble.
On the other hand, if you want to drive electrical geeks up the wall, just ignore all the above. Good luck!
One more thing – a small k for kilo, a capital W for Watts, and a small h for hour. Thanks.

 RSS - Posts
RSS - Posts


The kW v kWh debate is akin to the km\miles v kph\mph. Maybe your car can hit 200, but most places you’ll be limited to driving 100 or less. And while you can do perhaps 1,000 a day, that’s 10 hours of driving at 100 kph.
Or the parallel doesn’t help?
Hi George, yes but I find that using that particular analogy doesn’t help when trying to simplify things to get a concept across because the terms are too confusing. In the car analogy the rate (speed) is measured in km/h and with electricity, the rate (power) is measured in kW. With the car, the distance is measured in km, and in electricity, the *distance* (energy) is measured in kWh. The terms appear to be back to front and so can add another layer of confusion for people trying to wrap their heads around it. The only analogy I would use would be the hose (power) and bucket (energy) one, but I’ve purposely tried to keep analogies out of this article because my aim is to have the reader thinking in the same language that they’re speaking.
An analogy does nevertheless seem useful when it is a smaller step to fundamental understanding. And there’s nothing better than a horse for putting meat on these abstractions. Most people can understand that if you have one horse hitched to your cart, you have one horsepower,and with two horses there’s two horsepower you can giddyup. It’s not much of a stretch to one horse doing two horsepower-hours of work in two hours,and the two doing it in one. If hitched to your pool pump or a generator,they still have the same production of work = energy. The critical “time” distinction is established, in connection with energy and power.
All that remains is to scale the power unit. So let on that an electrical horsepower is near as dammit 3/4 kW, and that’s what a standard horse can do for 8 hours, producing 6 kWh of energy. For a shorter period, a kW would be no problem. So now a kW is a horse at a gallop, but a kWh would take longer than an hour, as he’d have to drop back to a trot, i.e. less than a kW before the hour is up. Tthe simple time relationship is also reinforced.
Many people have difficulty with quantifiable abstractions. Giving them relatable tangible substance can aid latching onto the significance of the time distinction in this case. I suspect that energy consumption of a washing machine or electric kettle is insufficiently kinetic to breach the imagination barrier, i.e. it’s already a bit too abstract to be the introductory concept.
All that said, saying “kW” instead of “kWh” is oddly frequently just a slip of the tongue, committed by folk who have learnt the difference, often more than once. (My preferred remedy is a quiet cup of coffee and a Timtam,)
I thought of the “horsepower” analogy too!
Also, what about car analogies….
Say a 4-cylinder Suzuki Swift versus a V8 BoganMobile.
If you drive from Upper Cumbucta West to Upper Cumbucta North, and it takes 1 hour, the Swift may use up 1/2 tank of petrol, whereas the V8 would use 2 tanks of petrol.
Car power (kW) and how much petrol it uses (kWh)….does that work?
in the context of battery, kW is how many toasters you can run at once, kWh is how long they will run for.
For those who did calculus at school, energy is actually the integral of power over time. (As distance is the integral of speed over time.) In the special case of constant power, this simplifies to the product. The average is the integral divided by the overall time. Hence the integral of power is the product of average power and overall time.
I always find that thinking integrals is easier, but then I did a lot of calculus.
Excellent article.
Now please ask the industry ( including software developers ) to use kWp when describing the capacity of a solar array.
kW and kWp tell two very different stories.
I’m sure you can explain why this is important.
I have noticed the confusion with kW and kWh for many years. In the ACT, where I live, an act was established in 2007 when they decided to offer feed-in-tariffs to households that installed solar panels. They made an error and set their tariff as a $ amount per kWh instead of kW. This error remained in the legislation until it was recently replaced. I have often wondered what would have happened if this had been challenged in court. I still have a copy of the 2007 legislation and often send it to other people to see if they can pick up the error; not many do.
Err, the tariff should be $/kWh. It is energy that you are buying or selling, even if to the “power” company. 😉
Yes, sorry I made a mistake. I realize the payment is $ / kWh. What I meant to say was that the rate paid was to be set by the size of the arrays. Here is the relevant part of the legislation:
“(a) if the total capacity of the generators is not more than 10kWh—at the premium rate; and
(b) if the total capacity of the generators is more than 10kWh, and not more than 30kWh—at 80% of the premium rate; and
(c) if the total capacity of the generators is more than 30kWh—at
75% of the premium rate.”
As you can see the total capacity of the generators is given as energy when it should be power. Sorry for the confusion.
*lie in it
Great article, thanks! I think I understand now…
Great article. Now could you try to educate economists who say things like
The debt-to-GDP ratio is the ratio between a country’s
government debt and its gross domestic product (GDP).
and
The Gross Domestic Product (GDP) in Australia was worth 1552.67
billion US dollars in 2021, according to official data from the World Bank.
where they actually mean annual GDP, GDP being a rate (so much per week, 52 times that per year, and so on), and government debt being an amount.
I guess you’d have a job ahead of you educating them, the second quote being from the World Bank