
If you own a good-sized solar power system, rising electricity prices are not a worry, in fact some solar owners will see their bills decrease thanks to rising feed-in-tariffs.
Australians don’t pay the highest electricity prices in the world, but we’re working on it.
For those embittered by Australia’s failure to take first place in the ‘pay-through-the-nose sweepstakes’, you’ll be glad to know further price increases on their way could allow Australia to become number one for most expensive electricity in the world!1
The reason electricity prices will be hiked yet again is because wholesale prices have soared2 and electricity retailers are going to pass this on to consumers. I’m sure they don’t want to, but when businesses are faced with a choice between making more money or not making more money, for some reason they always seem to go for more money.
The removal of subsidies in WA will lead to residential electricity prices rising by around 21% while in NSW, Queensland, Victoria, and South Australia soaring wholesale electricity prices will likely increase household bills by 20% or more, with NSW copping the biggest hike. The only silver lining is the pain will be spread out over the next 2 to 3 years3 and a large part of Victoria’s increase already occurred at the start of this year.
Because wholesale electricity prices have risen, solar feed-in tariffs will also increase, as wholesale prices are what feed-in tariffs are supposed to reflect. The feed-in tariff in Victoria will rise to a minimum of 11.3 cents on the first of July and feed-in tariffs of 10 cents or more are now available in NSW, QLD, SA, and the ACT. And there is talk of NSW going even higher in July.
Because both grid electricity and feed-in tariffs are going up, rooftop solar goes from being an amazing investment to a complete no brainer for almost anyone who owns a roof. It not only increases savings from any self consumed solar electricity, but increases the credits from selling any surplus solar back into the grid. A double whammy that increases solar owners’ savings even more.
But those who can’t install rooftop solar, which includes the poorest in our society, are going to get hurt.
WA Residential Prices Ready To Rocket
Because of the massive distance between Western Australia and the National Electricity Market (NEM) made up of the eastern states and South Australia, WA hasn’t suffered the same increase in wholesale electricity prices. But West Australians will still be screwed over because their State government is reducing the subsidy that hides the real cost of grid electricity from households and so their bills will rise by an estimated 7% a year over the next three years.
NT Price Increases Won’t Be So Bad
The Northern Territory has its own separate itty bitty grid4, or rather, a collection of separate little grids. Fortunately, the Flop End5 will be mostly protected from electricity price increases and, despite some problems, their bills may rise by less than 5% over the next two years.
The ACT Is Protected By Its 100% Renewable Electricity Target
Because the ACT has locked in long term electricity prices with renewable Power Purchase Agreements in preparation for meeting their 2020 100% renewable electricity target, they are reasonably well protected from electricity price increases and so should suffer a much smaller increase than NSW – the state they trapped inside.
Prices In NSW, QLD, SA, And VIC Will Soar
If National Electricity Market wholesale prices lived in a house, they’d need someone to come and fix the holes in the roof, because that’s what they’ve smashed through.
Unfortunately, it is not possible to know real wholesale prices in Australia. This is because a great deal of electricity is traded via contracts and those contracts have secret prices. But we can look at spot prices which is the how much electricity is traded for outside of contracts. Spot prices average slightly higher than wholesale prices. If they didn’t, there would be no point in having contracts. They also jump around a lot more. But they do reflect wholesale prices and are the most accurate indicator available.
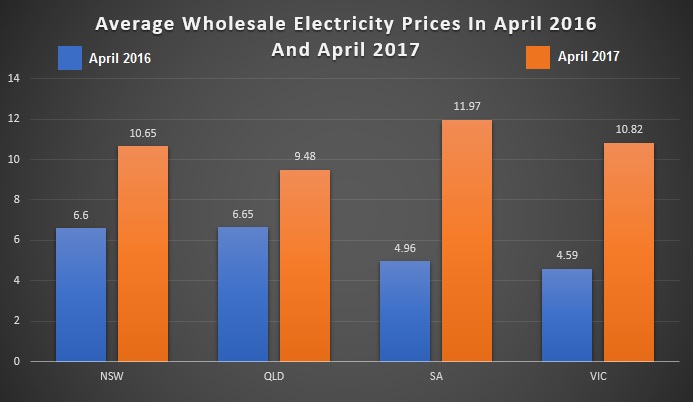
Average wholesale spot prices have soared in NSW, QLD, SA, and VIC, as the following skillfully made graph displays6. It shows the average wholesale spot prices in cents per kilowatt-hour in April last year compared to April this year:
As you can see, in South Australia and Victoria average wholesale spot prices have more than doubled.
Tasmania is not included in the graph because in April last year they were in the middle of an energy crisis thanks to having drained their hydroelectric dams just before they were hit by both a drought and a busted Basslink interconnector cable that pushed their average wholesale spot prices up above 23 cents a kilowatt-hour. But if we instead look at April 2015 we see the average wholesale spot price was 4.1 cents which was less than one-third the 13.1 cents it was this April.
Refining The Figures
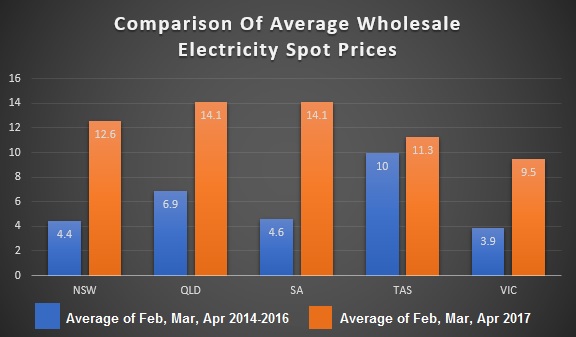
There is a considerable amount of variation in average wholesale electricity spot prices from month to month and year to year. To get a more accurate picture of how they have increased I have taken the average wholesale spot price for February, March, and April over the previous three years and compared it with the average for those three months this year. In cents per kilowatt-hour this gives:
Clearly, there have been massive increases everywhere except Tasmania on account of their energy crisis, with the average spot price more than tripling in SA.
One interesting thing about the graph is it shows during the previous three years the average spot price in renewable heavy South Australia was considerably lower than in coal dominated Queensland. This is not what you would expect if you believe coal is cheap and renewables expensive, as the Coal-ition keeps telling us.
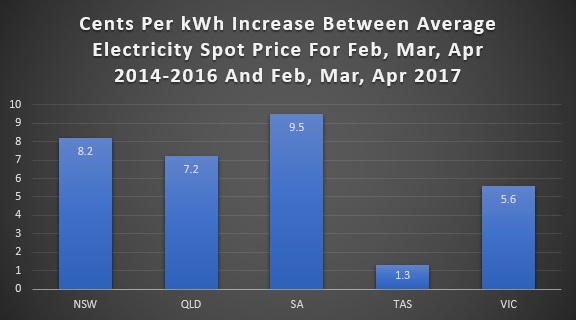
The difference between the average of the previous three years and the last three months in cents per kilowatt-hour comes to:
Fortunately, we won’t be charged this much extra per kilowatt-hour in the short term. But if wholesale electricity prices remain high enough for long enough, we will be.
The Future Is Far From Perfect
Normally when wholesale spot prices soar like this it is not unreasonable to assume it is just a blip and things will return to normal soon enough. Unfortunately, this is very unlikely to be the case. According to the electricity futures market, wholesale electricity prices will remain high for the next two years before we see any decrease and even then they should remain far above average for at least three years after that.
Morgan Stanley estimates7 residential electricity prices in NSW will increase by 20-25% and Victoria’s will rise by around 20% or more.
As Victoria’s residential electricity prices increased by almost 10% at the start of this year they are likely to see a further increase of around 10%.
Looking at future market prices, I see that both Queensland and South Australia are also likely to suffer large increases, with South Australia getting the worst of it.
The Price Hike Won’t Happen All At Once
Victorian electricity prices go up at the start of the year8, so they’ve already had a considerable increase, while other states, except possibly Tasmania, will be hit with large increases from the first of July. The slightly good news is the hikes won’t happen all at once and will probably spread out over two or three years. After that, prices will remain high until electricity retailers have recovered all the money they are entitled to under law and not a dollar less.
The reason why we’re not being hit with huge increase all at once is because retailers fear angry citizens. They don’t want people demanding politicians do their job and run the country more efficiently. They are well aware that if electricity production and distribution was nationalized, as it was decades ago, it could potentially halve the cost of providing electricity to households and leave electricity generators and retailers with only limited opportunities for profit. They also don’t want to create an even larger rush to install rooftop solar than what is already occurring.
Fixed Costs And Charges Per Kilowatt-Hour
As the cost of wholesale electricity has increased it seems reasonable to expect households to be hit with a straight increase in the charge per kilowatt-hour used. But electricity retailers may be much more devious than this and pass on some of the price increase in the form of higher fixed costs. There are 3 main reasons why they prefer to raise fixed costs:
- They are less noticeable to consumers than increases in cost per kilowatt-hour.
- They don’t encourage energy efficiency which reduces the amount of electricity sold.
- They don’t improve the economics of rooftop solar.
Hopefully regulators won’t let them get away with increased fixed costs. But if they do, as they have plenty of times before, then small users of grid electricity will have proportionately larger increases in their electricity bills than larger users.
Economic Justice Requires Lower Fixed Costs
Because a large portion of people who are small users of grid electricity are low income earners, any increase in fixed costs will mean that, on average, poorer people will be hit with a higher increase in the cost of electricity than richer people. I think this is blatantly unfair and I’m sure everyone will agree with me on this, with the possible exception of complete tossers.
In the interests of economic justice, I would like regulators to decrease fixed costs to reduce the impact of the coming electricity price hikes on low income households9, which will include many renters who are unable to install solar. I would prefer to see fixed costs eliminated, but any reduction would be an improvement.
Solar Feed-In Tariffs Will Increase
Wholesale electricity prices have risen and so solar feed-in tariffs will also rise, because feed in tariffs are meant to represent the average wholesale cost of electricity during the day.
Victoria’s feed-in tariff will rise to a minimum of 11.3 cents per kilowatt-hour from the 1st of July, while available feed-in tariffs have already increased in most other states.
Using the SolarQuotes electricity plan comparison tool, and ignoring the deceptive information Origin Energy provides10 for their Solar Boost plan, I see the highest feed-in tariffs available in NSW and the ACT is 10 cents, QLD 11 cents, and SA 12 cents. In Victoria Globird is currently offering 14 cents.
I don’t know if Tasmania’s regulated solar feed-in tariff will increase from its current 6.67 cents, but it definitely should. Mind you, solar households got screwed over in 2016 when Tasmanian wholesale electricity prices went through the roof during their busted Basslink energy crisis, so maybe they’ll get screwed over again come July. 11
Rooftop Solar Protects Households From Grid Price Rises
Households with small rooftop solar systems will be at least partially protected from grid electricity price increases, while households that produce more solar electricity than they consume in total will actually be better off.
For example if a solar home in NSW uses around 5,900 kilowatt-hours a year. With 5 kilowatts of north facing solar panels they can expect to produce around 6,900 kilowatt-hours of solar electricity. If both grid electricity prices and feed-in tariffs increase by 5 cents then their electricity bills will go down by $50 a year.
Solar Is Now Essential For Almost Everyone With A Roof
Rooftop solar was the pretty much the best investment most households could make, but now it has almost become essential for everyone whose hobby isn’t flushing money down the toilet. With the current low cost of installing a high quality solar system, the increased feed-in tariffs now available to most Australians, and the coming electricity price rises, you’d have to be nuts not to install solar if you own a roof.
Higher electricity prices and feed-in tariffs mean that attempting to properly size a rooftop solar system is no longer an issue. It now makes economic sense to install as large a solar system as you are permitted in your area and that your roof will allow. Higher feed-in tariffs mean north facing panels will normally be best, but east and west are also suitable and even south facing panels can be profitable.
The only major exception where it may not make sense to install solar is if your roof is heavily shaded. But even then it’s probably a good idea to check to see if you can still come out ahead.
Why Are Electricity Prices Increasing?
One thing I haven’t done is write about why wholesale electricity prices are increasing. A simple answer is because generators have been able to get away with charging more. A less simple answer is a whole other article I will soon get around to writing.
At some point I will also write about how the coming increases in grid electricity prices won’t improve the economics of batteries because the advantage of higher prices are cancelled out by higher solar feed-in tariffs.
Footnotes
- This is only likely to be before taxes are applied, but you can’t have everything. ↩
- in most states ↩
- The reason retailers will raise prices over a number if years is not out of the kindness of their hearts. They are hoping to avoid any dummy spitting that could cost them money in the long run. An example of a recent high velocity dummy spit is the Weatherill government in South Australia deciding to build its own battery storage and a 250 megawatt gas plant. ↩
- The Northern Territory only has 8,800 km of power lines and 40,000 poles. This means they only have one pole per 220 meters of power line. Fortunately it’s not as bad as it sounds as you can stick more than one power line on a pole and they place one-third of their lines underground one account of how God keeps trying to destroy Darwin — one time with successful help from Imperial Japan. ↩
- With the highest average household size in the country and a large transient population crashing on couches, the Nothern Territory is the floppiest place in the nation. ↩
- This graph was made by a robot, which means my 10 year old is now out of a job. If you see him out begging, please give generously. (I promise I’ll only take a small cut.) ↩
- I’d provide a link to Morgan Stanley’s research, but I’m afraid that it’s behind a wall that even my tricks can’t get behind. (Paying subscription fees is not one of my tricks.) Fortunately, Morgan Stanley was kind enough to simply tell us the information. ↩
- Technically, they can also go down at the start of the year, but that rarely seems to happen for some reason. ↩
- Reducing fixed costs will also improve the economics of rooftop solar, but that is not a bad thing. ↩
- I originally wrote that the highest feed-in tariffs available were from Origin Energy, based on the 12 cent feed-in tariff they provide with their Solar Boost plan. Fortunately, Ray Cooper pointed out in the comments that only applies for people who have a new solar system installed by Origin. (Thanks for that Ray.) The best solar feed-in tariff Origin Energy offers that isn’t part of a sales gimmick is 10 cents and that is available in NSW, QLD, SA, and the ACT. ↩
- When it comes to the Tasmanian government I sometimes get the impression the left head doesn’t know what the right head is doing. ↩

 RSS - Posts
RSS - Posts


It appears as though you are required to buy a new solar power system from Origin to be eligible for 12c feed in tariff. This opens up a few value for money considerations. Origin offers 10c for the rest of us but drops their discount on power usage from 12% to 5%. God bless them. It can work out cheaper for a small number of low power users with a large PV system, but most of us would be paying more compared with a better discount on usage and 6c feed in tariff..
Yes, and as for Click offering 12c FiT have a look at their Off-peak rate. It’s 24c kWh. I’m better of over at EnergyAustralia as it’s 14c kWh even with the lower 8.2c FiT. If you don’t have Off-peak requirements then Click may be the way to go. Daily connection charge is 84c for Click and 79c for EnerygyAustralia. I put all the plans into a spread sheet to compare.
I went through the process a few weeks ago. SE Qld. Have a fairly high power usage with 6.5kW solar. My spreadsheet showed Energy Australia was the best with 16% discount on non-inflated tariffs and 6c FIT. Click wasn’t in the ballpark – All tariffs and daily service fee were inflated. The story of Peter and Paul.
Thank you very much for that, Ray. I have corrected the article and I will now see if there is any way to stop Origin Energy’s Solar Boost Plan as being displayed as having a 12 cent feed-in tariff, as that does not apply under normal circumstances.
Isn’t the Solar Boost plan a 10 Months benefit period? What happens after that expires?
Origin Energy’s Solar Boost plan is a 12 month contract. At the end of that you either renew the contract or you change to whoever offers a better overall deal. There is a good chance that in a year you will be able to do better than a 10 cent feed-in tariff.
Of course, many people won’t realize their contract is ending and so will lose money. This is just one of the tricks commonly used by electricity retailers to get people to sign up to a plan that seems good and then milk them for extra money later.
I loved the article but most disappointed that there was nothing regarding WA.
Hello Delma. The article does mention that Western Australia’s residential electricity prices are expected to rise by an estimated 21% over the next three years due to the state government subsidy being cut.
(under the heading ” the ACT is protected by….” Methinks you need to look at the map again as to which of ACT?NSW encompasses which!
Hi Ronald, once again another well detailed article from you. I have a few thoughts.
North facing panels may not be the smartest answer when T-FIT becomes an option. Sure, they’re more efficient in terms of output but unless you self consume a large portion of your daytime generation with a T-FIT west facing panels may generate more income for those who are at work until sunset.
Both baseload and peaking contracts have increased significantly. Taking 1600MW of baseload out of Victoria was always going to have consequences, and largely in part to PV infiltration peak loads are occurring later in the day and demanding higher ramp rates. Unless the wind is blowing this is where hydroelectric and open cycle gas will play a larger role in coming years, as well as distributed batteries. Although gas is becoming an increasingly expensive form of generation it is vital measure to ensure security of supply during these times where alternatives are unavailable or impractical.
I do respectfully disagree with your views on supply charges. Even if you generate and self consume your PV to a degree where your bills are negligible you’re still enjoying the benefit of a reliable and resilient grid at night and when the weather is overcast. This all takes resources. Your PV exports are facilitated by distribution upgrades to allow bidirectional flows over the network and benefit other consumers. Throwing all the emphasis on the consumption charge will first raise the unit charge to a point where large consumers realise they can move off grid and self generate. This is already happening on some large farms where diesel is cheaper. Without these large users on grid cross subsidising energy misers the charges will skyrocket even further – renters, pensioners and those not financially well off will wear the full cost. Network charges being metered separately allows appropriate levels of network investment to occur while still charging the energy component as appropriate.
To allow large uptake of renewable, intermittent sources of energy transmission and distribution networks need to be bolstered. I personally feel PV owners (for the record that includes me) aren’t truly being charged accordingly. As mentioned renters and pensioners – those in no financial position – could have a lower fixed charge while those that can afford to throw a few thousand at panels might pay a bit more.
The future is rather uncertain and lack of consistent federal and state direction isn’t helping. The draft QCA determination is showing a decrease in the service charge and an increase in the consumption charge for the next financial year, but not significant. At this stage good news for distributed generation but we’ll need to see how politics pans out.
tsk tsk tsk!
Righto children; say after me:- B….A…T…T…E….R…..Y! LEAD-ACID. STAND-ALONE!! YAYYY!!!
How absurd has the whole merry-go-round become when it’s seriously suggested that one goes to the trouble of setting up an expensive solar system …..and then deliberately run it in less-than-most efficient-mode???
Why not buy a million-dollar house and then sleep in the backyard?
Fair dinkum people!
The only realistic options are:- (a) Get together and wield your economic power to whip power suppliers AND governments into line , or (b) Go independent with (relatively-dirt-cheap) lead-acid storage….and threaten to sool Tonto 23 onto any bastard that comes up with the idea of taxing/selling sunlight.
It’s YOUR money Ralph!……and THEY want it. A better use for it might be to fund a civil insurrection….Oz is the only country in the world that’s never staged a revolution. Perhaps the fore-lock-tugging subservience of our criminal heritage has been embedded in our genes.
Jack, if you can give links to professionals who are installing relatively-dirt-cheap lead-acid battery systems that will let people save money by going off-grid while providing a similar level of comfort and convenience that being on-grid provides, I will check them out and write up articles about them if they are fair dinkum. But I am not aware of the existence of any. Most people lack the knowledge and skill required to set up their own lead-acid battery systems and they will not be able to save money by paying someone else to install one.
They also won’t be able to save money with any other battery chemistry at the moment either, as I’ve pointed out a few times.
So, here you have it today.
ALG has announce a 16 per cent rise on the 1st of July , not spread over years as suggestedd, but a one off hit.
The other revelation *(but not to me) is the cost of electricty to NSW consumers per annum.
This came in at $2,200.00
After reading some of these posts one would believe that consumption per annum is less than $800.00.
Once again I reiterate about the size of storage batteries needed to over come these spiralling costs.
The size is much larger than expected probably 2 to 3 times what you are thinkging.
Look at the last 3 days, total solar generated on a 6KW system was 12 KW .
usage was 18KW a day which falls inline with the $2,200 cost of power.
And no comment of an increase in feed back tariff.
C’mon Ron what’s going on ?????
A 16% increase is a huge slug, but you are in NSW so they will hit you again next year with another one. If AGL is not giving you a decent feed-in tariff I suggest shopping around. Their main competitor, Origin, is offering 10 cents and other retailers are offering more, but care is required as chasing higher feed-in tariffs can result in paying more overall.
I am with Click in NSW and this is my July price rise.
Domestic Tariff – 31% increase.
Off-Peak Tariff – 90% increase.
Service Charge – 1% decrease.
Solar FIT – 17cents per kilowatt.
The Off-Peak Tariff was increased by 50% in July 2016. So a 200% increase in 13 months.
AGL of course
Oh, and further to my comment I just checked with Agl and no comment on an increase but the VIC govt.announced a minimum increase from 5 cents to 6.5 cents wowo !!!!! gig effen deal .
Another thing that users may not be aware off.
if you are stuck on a plan that gives you 16% discount for on time payment that will not change unless you the consumer goes onto your account and change plans.
I mention this because AGL offer 4 rates 14% 16% 18% and 22% and after i checked the terms and conditions i can find not one single difference.
Latest update from regional QLD… Tariff 11 rising approximately 3.5% but FIT going up about 30%! Even with a modest system many will see their bills go backwards. We have a 2.5kW system and expecting a net decrease of about $30 a quarter based off prior usage and exports.
As for my earlier comments regarding T-FIT the QCA are running some figures and it doesn’t look good for most. Unless you have a large west facing array and don’t use the output at dusk it’s not viable under the majority of models.
Update as of August 2017.
Alinta are offering 25% discount on usage with decent connection costs and 11c FIT.
Quick calcs for us were about $250 quarter – with 2500kWh usage / 26kWh solar generated per day and 40% daytime usage.
Before Solar we were paying $650 quarter via Origin Maximiser.
Origin Solar Boost (not Origin Boost plus – where you need to buy the solar system from a pseudo Origin badged sales company) is the next best deal for use at about $275 quarter.